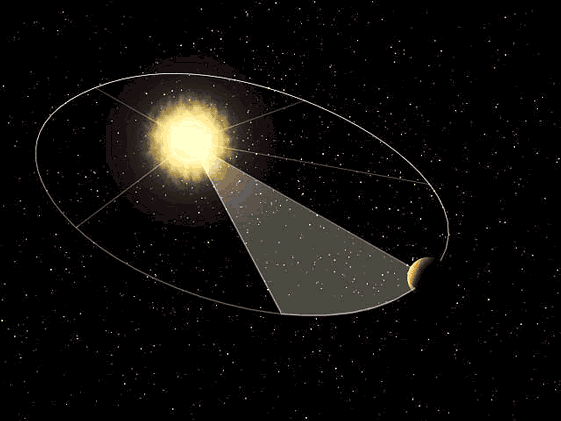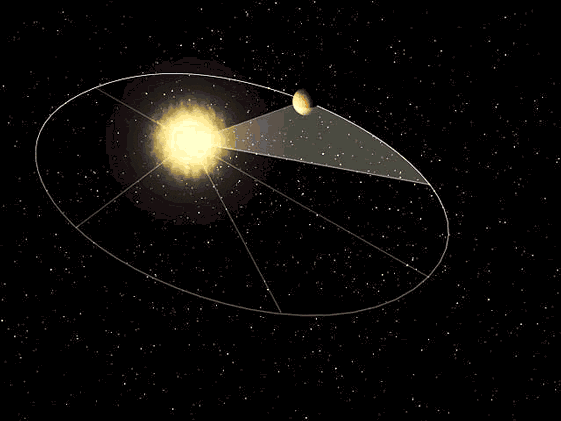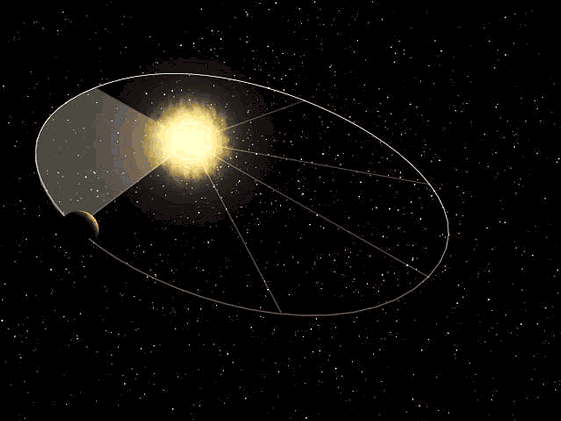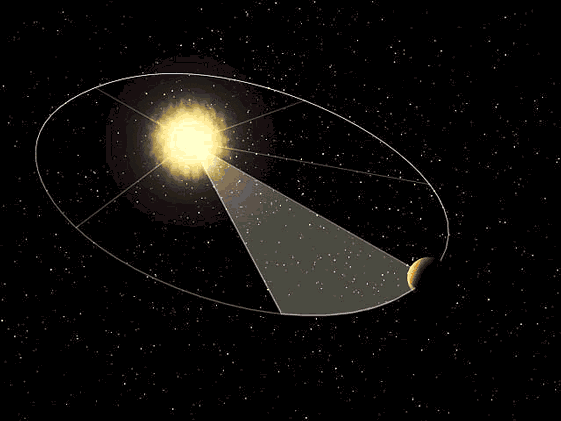
. ALONDRA y VALERIA viajan en el camión. Al detenerse, sintieron que se impulsaban hacia
adelante. Esto se debe a:
a) La fuerza de gravedad
b) La inercia
c) Por la fuerza de fricción
d) No pagaron el pasaje
- Cuando empujas el carrito de mandado, este se mueve, pareciendo que devuelve la fuerza. A estas fuerzas se les conoce como:
- Cuando empujas el carrito de mandado, este se mueve, pareciendo que devuelve la fuerza. A estas fuerzas se les conoce como:
a)
Acción y reacción
b) Gravedad
y acción
c) Empuje y atracción
d) Fricción y
resultante.
- En
una discusión en clase, se pretendía señalar ejemplos de la fuerza de fricción.
Escoge la respuesta correcta:
a) Sin la
fricción resbalaríamos fácilmente en cualquier superficie
b) La forma
de los aviones permite una mayor fricción para volar
c) En superficies
lisas no hay fricción
d) Los patines en cemento eliminan la fricción.
-La aceleración de la gravedad en la tierra es
de 9.81 m/s2 y en Marte 3.71m/s2. Juan Pablo tiene una masa de 60 kg. ¿Cuál será el
peso de Jorge en Marte? F=ma
a) 222.
b) 6 N
c) 300 N
d) 200 N
e) 400 N.
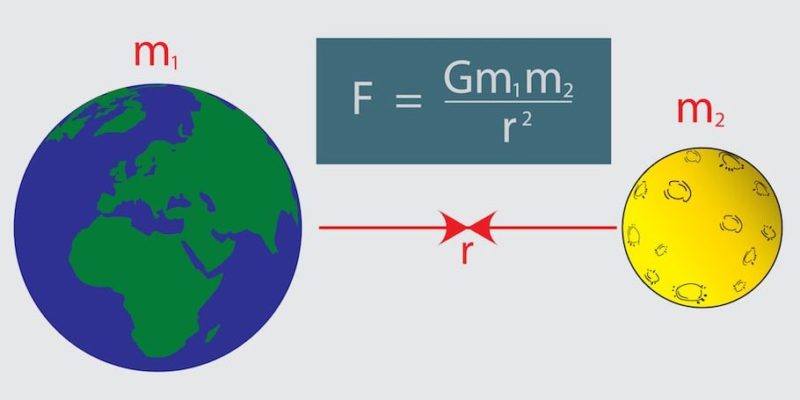
Calcula la fuerza gravitatoria entre el Sol y la Tierra.
Datos:
Mtierra= 6 x 1024 kg
Msol = 2 X 1030 kg
R = 150 X 109 m
2. ¿Cuál sería la fuerza gravitatoria si la distancia fuera del doble?
3. Calcula el peso, en cada planeta y en la Luna, para una persona de 70 kg de masa.
Datos:
gTierra = 9.8 m/s2
gLuna = 1.62 m/s2
4. ¿Cambia su peso en cada planeta?
5. ¿Cambia su masa en cada planeta
6. Un objeto pesa 125N en la superficie terrestre. Calcula su masa.
-La carrera espacial del Discovery llegó a su fin. Su último vuelo fue la
misión STS-133, del 24 de febrero de
2011. Aterrizó al mediodía en Florida tras una misión de 13 días. La nave
estuvo 27 años en actividad y ahora se exhibe en un museo. La NASA espera
lanzar el vehículo de exploración tripulado Orión en el nuevo cohete Ares I
antes del 2014.
Es
todo un espectáculo ver como la nave se lanza hacia el espacio y la quema de
combustible y así como sus desechos hacia el lado contrario (hacia el suelo).
La propulsión del lanzamiento de la nave es un ejemplo práctico de la:
A) Primera
Ley de Newton.
B)
Segunda Ley de Newton.
C)
Tercera Ley de Newton.
D) Caída
libre de los cuerpos.
-Los cuerpos celestes se
mueven en el vacío, más no en línea recta, tal es el caso de la Tierra que
sigue una trayectoria curva alrededor del Sol. Lo mismo sucede con la Luna,
quien sigue una trayectoria curva alrededor de la Tierra.
¿Cuál es la ley que rige
a los astros del Universo para que siempre se mantengan a cierta distancia y en
órbitas determinadas?
A) Primera Ley de Kepler.
B) Segunda Ley de Kepler.
C) Tercera Ley de Newton.
D) Ley de la gravitación Universal.
-Relaciona
las dos columnas para ejemplificar correctamente los dos tipos de fuerzas.
I.-
Fuerzas a distancia
II.-
Fuerzas de contacto
|
a.-
Órbita de la Tierra alrededor del Sol
b.-
Patear un balón
c.
Atracción entre dos cuerpos
d.-
Fricción del aire que detiene un avión
|
Escoge
la respuesta correcta
A)I-a y I-b; II-c y
II-d
B)I-a y I-c; II-b y
II-d
|
C)I-a y I-d; II-b y
II-c
D)I-b y I-c; II-a y
II-d
|
-Son las características de un vector:
A) Distancia, masa,
velocidad y tiempo
B) Origen o punto de
aplicación, valor o tamaño, dirección y sentido.
C) Flecha, ángulo de
inclinación, punto cardinal y resultante
D) Escala adecuada, localización, plano cartesiano
y sentido.
-Dos fuerzas de igual magnitud se
aplican en un mismo punto y forman un sistema vectorial concurrente; si una
fuerza se aplica al Este y la otra al Norte, ¿cuál de las siguientes gráficas
representa al vector resultante?
-Un jugador patea un balón con una fuerza de 250 N desde 20 m a la portería
formando un ángulo de 60° con un costado de la cancha; en vectores ¿Qué
representa el ángulo de inclinación?
A) El Sentido C)
La Longitud
B) La Dirección D) La Magnitud
-La
masa de un estudiante en la Tierra es 60 Kg y pesa 60 Kg-fuerza, ¿Cómo serán
estos valores en la Luna donde la fuerza de gravedad es la sexta parte (1/6) de
la fuerza gravedad de la Tierra.
A)
La masa será la misma y el peso será 6 veces mayor.
B)
La masa será la misma y el peso será 6 veces menor.
C)
La masa será 6 veces mayor y el peso será el mismo
D)
La masa será 6 veces menor y el peso será el mismo.
-Selecciona
las aseveraciones correctas:
I.-
Cuerpo de mayor densidad que un fluido: flota
II.-
Cuerpo de menor densidad que un fluido: se hunde
III.-
Cuerpo de menor densidad que un fluido: flota
IV.-
Cuerpo de mayor densidad que un fluido: se hunde
V.-
Cuerpo con igual densidad que un fluido: se queda en equilibrio donde se le
deje.
A)
I, II
y III
|
C)
III, IV y V
|
B)
II, III y IV
|
D)
I, III
y IV
|
*-¿Qué ocupa más volumen, 150 Kg de varilla de
Acero ó 150 Kg de varilla de Bronce? La densidad del acero es de 7.9 Kg/litro y
la densidad del bronce es de 11 Kg/litro
A)
La de acero porque tiene más
masa por litro
B)
La de bronce porque tiene
menos masa por cada litro
C)
La de acero porque ocupa más
volumen por cada kilogramo
D)
La de bronce porque ocupa más
volumen por cada kilogramo
-¿Cuál será la fuerza que requiere
aplicar un ciclista para acelerar su bicicleta a 15 m/s2, si la masa
del ciclista y la bicicleta es de 70kg?
-. Cuando caminas interaccionas con el piso a través de la fricción,
¿quién recibe la acción y quién la reacción?
- Relaciona las dos columnas. Escribe dentro del
paréntesis la letra de la respuesta correcta
( ) Ley de Gravitación Universal
( ) Tercera Ley de Newton.
( ) P = mg
( ) a = F / m
( ) Ley de la inercia
|
a) A toda acción
corresponde una reacción de igual magnitud, igual dirección, pero de sentido
contrario
b) La aceleración
que experimenta un cuerpo al aplicarle una fuerza es directamente
proporcional a la fuerza aplicada e inversamente proporcional a la masa del
objeto
c) Todo cuerpo que
está en reposo o en MRU permanece en reposo o en MRU a menos que una fuerza
externa modifique el estado inicial
d) “La fuerza con que se atraen dos objetos es
proporcional al producto de sus masas e inversamente proporcional al cuadrado
de la distancia que los separa”.
e) Es la fuerza
con que la Tierra atrae a todos los cuerpos que se encuentran en su
superficie hacia el centro de ella
|