Vectores y Escalares. Física.
Suma Gráfica y Analítica
En física debemos distinguir entre vectores y escalares.
Un vector es una cantidad orientada, tiene tanto magnitud como dirección.
La velocidad, la fuerza y el desplazamiento son vectores.
El tiempo, la temperatura y la energía son escalares: sólo tienen magnitud, no tienen dirección asociada a ellas.
Los vectores se representan mediante flechas, en que la longitud de la flecha se traza proporcionalmente a la magnitud del vector. Las letras que representan vectores se escriben en negrita.
1.- Suma de Vectores. Método Gráfico
Para sumar escalares, como tiempo, se usa la aritmética simple. Si dos vectores se encuentran en la misma recta también podemos usar aritmética, pero no así si los vectores no se encuentran en la misma recta. Por ejemplo, si Ud. se desplaza 4 km hacia el este y luego 3 km hacia el norte, su desplazamiento neto o resultante respecto del punto de partida tendrá una magnitud de 5 km y un ángulo = 36.87º respecto del eje x positivo. Ver figura
= 36.87º respecto del eje x positivo. Ver figura
Para sumar escalares, como tiempo, se usa la aritmética simple. Si dos vectores se encuentran en la misma recta también podemos usar aritmética, pero no así si los vectores no se encuentran en la misma recta. Por ejemplo, si Ud. se desplaza 4 km hacia el este y luego 3 km hacia el norte, su desplazamiento neto o resultante respecto del punto de partida tendrá una magnitud de 5 km y un ángulo
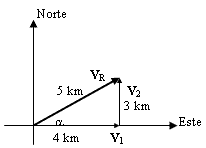
Vectorialmente, el desplazamiento resultante VR, es la suma de los vectores V1 y V2, o sea, escribimos VR = V1 + V2 Esta es una ecuación vectorial.
La regla general para sumar vectores en forma gráfica (con regla y transportador), que de hecho es la definición de cómo se suman vectores, es la siguiente:
(1) Use una misma escala para las magnitudes.
(2) Trace uno de los vectores, digamos V1
(3) Trace el segundo vector, V2, colocando su cola en la punta del primer vector, asegurándose que su dirección sea la correcta.
(4) La suma o resultante de los dos vectores es la flecha que se traza desde la cola del primer vector hasta la punta del segundo.
(1) Use una misma escala para las magnitudes.
(2) Trace uno de los vectores, digamos V1
(3) Trace el segundo vector, V2, colocando su cola en la punta del primer vector, asegurándose que su dirección sea la correcta.
(4) La suma o resultante de los dos vectores es la flecha que se traza desde la cola del primer vector hasta la punta del segundo.
Este método se llama suma de vectores de cola a punta.
Notemos que V1 + V2 = V2 + V1, esto es, el orden no es importante.
Notemos que V1 + V2 = V2 + V1, esto es, el orden no es importante.
Este método de cola a punta se puede ampliar a tres o más vectores. Suponga que deseamos sumar los vectores V1, V2, y V3 representados a continuación:
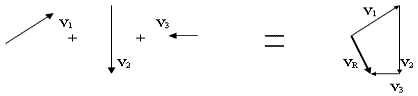
VR = V1 + V2 +V3 es el vector resultante destacado con línea gruesa.
Un segundo método para sumar dos vectores es el método del paralelogramo, equivalente al de cola y punta. En este método se trazan ambos desde un origen común y se forma un paralelogramo usando los dos como lados adyacentes. La resultante es la diagonal que se traza desde el origen común.
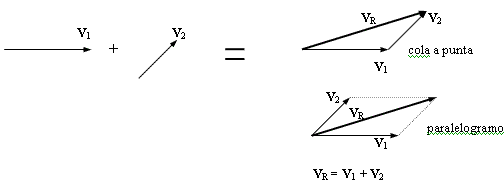
Operaciones con Vectores por el Método del Polígono
Éste es el método gráfico más utilizado para realizar operaciones con vectores, debido a que se pueden sumar o restar dos o más vectores a la vez.
El método consiste en colocar en secuencia los vectores manteniendo su magnitud, a escala, dirección y sentido; es decir, se coloca un vector a partir de la punta flecha del anterior. El vector resultante esta dado por el segmento de recta que une el origen o la cola del primer vector y la punta flecha del último vector.
Ejemplo. Sean los vectores:
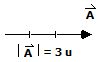
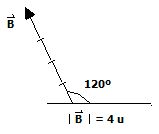
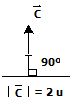
Encontrar 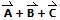 .
.
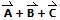 .
.
Resolviendo por el método del polígono, la figura resultante es:
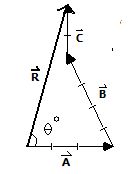
Si se utilizan los instrumentos de medición prácticos, se obtiene que :
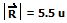
y que θ es aproximadamente 80°.
No hay comentarios:
Publicar un comentario