Guía examen noviembre

MRUA  y Caída Libre

Problema n° 1) Desde el balcón de un edificio se deja caer una manzana y llega a la planta baja en 5 s.

a) ¿Desde qué piso se dejo caer, si cada piso mide 2,88 m?

b) ¿Con qué velocidad llega a la planta baja?

Problema n° 2) Si se deja caer una piedra desde la terraza de un edificio y se observa que tarda 6 s en llegar al suelo. Calcular:

a) A qué altura estaría esa terraza.

b) Con qué velocidad llegaría la piedra al piso.

Problema n° 3) ¿De qué altura cae un cuerpo que tarda 4 s en llegar al suelo?

Problema n° 4) Un cuerpo cae libremente desde un avión que viaja a 1,96 km de altura, cuánto demora en llegar al suelo?

Problema n° 5) Un cuerpo cae libremente desde el reposo. Calcular:

a) La distancia recorrida en 3 s,

b) La velocidad después de haber recorrido 100 m,

c) el tiempo necesario para alcanzar una velocidad de 25 m/s,

d) el tiempo necesario para recorrer 300 m, desde que cae.

3. Problemas de MRUA

Problema 1

Describir el movimiento de la siguiente gráfica y calcular $v\left(0\right)$, $v\left(4\right)$, $v\left(10\right)$ y $v\left(15\right)$:

---

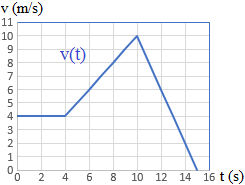
Problema 2

Elegir la gráfica de la velocidad en función del tiempo que se corresponde a cada situación.
Gráfica a:

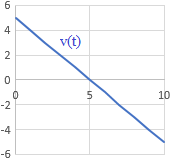Gráfica b:

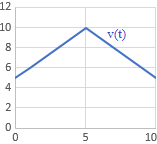Gráfica c:

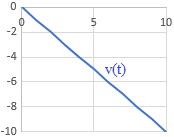Situaciones:

1. Dejar caer una moneda desde la azotea de un edificio: el movimiento comienza en el momento en el que se suelta la moneda y termina cuando ésta llega al suelo.
2. Lanzar una moneda hacia arriba en línea recta: el movimiento comienza cuando se suelta la moneda y termina cuando cae al suelo.
3. Efectuar un adelantamiento a un auto en marcha con otro auto: el movimiento comienza justo antes de realizar el adelantamiento y termina cuando, una vez rebasado el auto, se lleva la misma marcha que al inicio.

---

Problema 3

Calcular la aceleración (en $m/s^2$) que se aplica para que un móvil que se desplaza en línea recta a 90.0 km/h reduzca su velocidad a 50.0 km/h en 25 segundos.
Comentar el resultado.

---

Problema 4

Un tren de alta velocidad en reposo comienza su trayecto en línea recta con una aceleración constante de $a=0.5m/s^2$. Calcular la velocidad (en kilómetros por hora) que alcanza el tren a los 3 minutos.

---

Problema 5

Calcular la aceleración que aplica un tren que circula por una vía recta a una velocidad de 216.00km/h si tarda 4 minutos en detenerse desde que acciona el freno.

---

Problema 6

Un ciclista que está en reposo comienza a pedalear hasta alcanzar los 16.6km/h en 6 minutos. Calcular la distancia total que recorre si continúa acelerando durante 18 minutos más.

---

Problema 7

En una carrera cuyo recorrido es recto, una moto circula durante 30 segundos hasta alcanzar una velocidad de 162.00km/h. Si la aceleración sigue siendo la misma, ¿cuánto tiempo tardará en recorrer los 200 metros que faltan para rebasar la meta y a qué velocidad lo hará?

---

Problema 8

Dejamos caer una moneda desde una altura de 122.5 metros. Calcular el tiempo que tarda en posarse sobre el suelo.
Nota: la gravedad es $g=9.8m/s^2$.

---

Problema 9

Desde 600 metros de altura se lanza hacia el suelo una botella de cristal con una velocidad inicial de $18.36km/h$. Calcular la velocidad de la botella en el instante previo de romperse contra el suelo.

---

Problema 10

Un estudiante de física dispara una pistola lanza-pelotas en línea recta desde el suelo. Según las especificaciones de la pistola, la velocidad de lanzamiento es de $29.4m/s$.
Calcular la altura que alcanza la pelota y el tiempo que tarda en caer al suelo desde que se dispara.

Ejemplo 11:

Un tiburón tigre neurótico inicia desde el reposo y aumenta su rapidez de manera uniforme hasta 12 metros por segundo en un tiempo de 3 segundos.
¿Cuál fue la magnitud de la aceleración promedio del tiburón tigre?

12. Realiza un dibujo de una onda y escribe todos sus elementos

13. Describe las propiedades de las ondas como: reflexión, refracción y difracción.