La suma gráfica de vectores puede realizarse de dos maneras:
Vamos con la primera forma:
1 – Tenemos los vectores u y v:

Queremos sumar gráficamente v+u. Por tanto, colocamos el origen de u en el extremo de v:

Unimos el origen de v con el extremo de u y obtenemos el vector resultante v+u:

Intenta tú mismo realizar la suma gráfica de u+v y verás que el resultado es el mismo ;).
Vamos con la segunda forma de sumar vectores gráficamente:
2 –
Operaciones con Vectores por el Método del Paralelogramo
Para utilizar métodos gráficos en la suma o resta de vectores, es necesario representar las cantidades en una escala de medición manipulable. Es decir, podemos representar un vector velocidad de 10 m/s hacia el norte con una flecha indicando hacia el eje y positivo que mida 10 cm, en la cual, cada cm representa una unidad de magnitud real para la cantidad (1 m/s).
El vector que resulta de operar dos o más vectores, es conocido como el vector resultante, o simplemente la resultante .
El método del paralelogramo permite sumar dos vectores de manera sencilla. Consiste en colocar los dos vectores, con su magnitud a escala, dirección y sentido originales, en el origen, de manera que los dos vectores inicien en el mismo punto.
Los dos vectores forman dos lados adyacentes del paralelogramo. Los otros lados se construyen trazando líneas paralelas a los vectores opuestos de igual longitud.
El vector suma resultante se representa a escala mediante un segmento de recta dado por la diagonal del paralelogramo, partiendo del origen en el que se unen los vectores hasta la intersección de las paralelas trazadas.
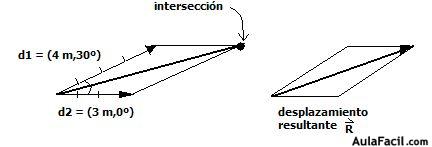
Ejemplo. Una bicicleta parte desde un taller de reparación y se desplaza (4 m,30º) y luego (3 m, 0º). Encuentre el desplazamiento total de la bicicleta, indicando la dirección tomada desde el taller.
El desplazamiento total se da en dos tramos. Cada tramo desplazado se representa por los vectores d1 y d2. El desplazamiento total es D = d1 y d2.
Los dos vectores son dibujados a la misma escala, y se colocan en el mismo origen. Luego se trazan las líneas paralelas.
Si medimos con una regla, a la escala dada, el tamaño del vector resultante debe dar aproximadamente 6.75 unidades de la escala; es decir, la magnitud del vector desplazamiento total es de 6.75 m.
La medida de la dirección se toma con la ayuda de un transportador, y debe dar aproximadamente 17º desde el origen propuesto.
El sentido del vector resultante es positivo, según el marco de referencia común (plano cartesiano, hacia x positivo y hacia y positivo). Entonces como resultado, la bicicleta se desplaza (6.75 m,17º).
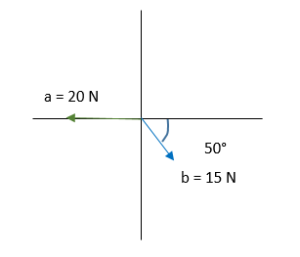
Tenemos los siguientes vectores:
Este ejercicio lo resolveré por el método del paralelogramo;
Ahora trazamos los dos vectores desde el mismo origen y formamos un paralelogramo trazando líneas paralelas a los vectores, la resultante es la diagonal que se traza desde el origen.
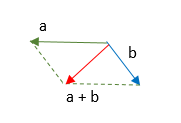
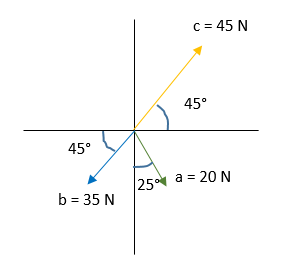
Tenemos los siguientes vectores:
Este ejercicio lo resolveré por el método cola a punta;
Seguimos las reglas generales de este método:
- Usar la misma escala para todos los vectores
- Trazar un vector (el orden no es importante)
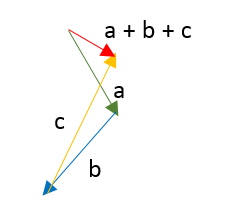
- Trazar el segundo vector, empezando desde el final del primer vector (la punta de la flecha), hay que dibujar correctamente el vector cuidando el ángulo, longitud y sentido.
- La suma de los dos vectores es la flecha que se traza desde el principio del primer vector hasta la punta del segundo.
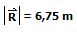
No hay comentarios:
Publicar un comentario