Semana del 26 al 29 de Octubre 2015

LEYES DE NEWTON

PRIMERA LEY DE NEWTON

La primera ley de Newton, conocida también como Ley de inercía, nos dice que si sobre un cuerpo no actua ningún otro, este permanecerá indefinidamente moviéndose en línea recta con velocidad constante (incluido el estado de reposo, que equivale a velocidad cero).

Como sabemos, el movimiento es relativo, es decir, depende de cual sea el observador que describa el movimiento. Así, para un pasajero de un tren, el interventor viene caminando lentamente por el pasillo del tren, mientras que para alguien que ve pasar el tren desde el andén de una estación, el interventor se está moviendo a una gran velocidad. Se necesita, por tanto, un sistema de referencia al cual referir el movimiento. La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se observa que un cuerpo sobre el que no actua ninguna fuerza neta se mueve con velocidad constante.

En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial.

SEGUNDA LEY DE NEWTON

La Primera ley de Newton nos dice que para que un cuerpo altere su movimiento es necesario que exista algo que provoque dicho cambio. Ese algo es lo que conocemos como fuerzas. Estas son el resultado de la acción de unos cuerpos sobre otros.

La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:

F = m a

Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse como:

F = m a

La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2, o sea,

1 N = 1 Kg · 1 m/s2

La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación F = m · a. Vamos a generalizar la Segunda ley de Newton para que incluya el caso de sistemas en los que pueda variar la masa.

Te dejo el siguiente prezi para que comprendas mejor la segunda Ley de Newton

http://prezi.com/hhzjbsb6tdmk/segunda-ley-de-newton/

Este experimento háganlo bajo la supervisión de un adulto o lleven el material a la escuela y lo hacemos en clase. Gracias.

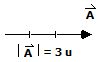
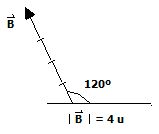
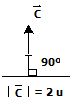
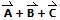Semana del 19 al 23 Octubre 2015

Experimento: Coche con motor de aire.

Aquí les dejo este video para que construyan su carrito impulsado por aire aplicando la Primera Ley de Newton. Si lo hacen, les doy 50 participaciones.

La Primera Ley de Newton (Ley del movimiento) - Física Entretenida

primera ley de newton

Semana del 12 al 16 de Octubre 2015

Operaciones con Vectores por el Método del Polígono

Éste es el método gráfico más utilizado para realizar operaciones con vectores, debido a que se pueden sumar o restar dos o más vectores a la vez.

El método consiste en colocar en secuencia los vectores manteniendo su magnitud, a escala, dirección y sentido; es decir, se coloca un vector a partir de la punta flecha del anterior. El vector resultante esta dado por el segmento de recta que une el origen o la cola del primer vector y la punta flecha del último vector.

Ejemplo. Sean los vectores:

Encontrar .

Resolviendo por el método del polígono, la figura resultante es:

Si se utilizan los instrumentos de medición prácticos, se obtiene que :

y que θ es aproximadamente 80°.

No dejes de checar la página de tareas para ver los materiales que te pido para Laboratorio y  el Proyecto del 1er Bimestre.

Semana del 5 al 9 de Octubre 2015

Tema 3. La descripción de las fuerzas en el entorno

Te dejo el siguiente link  de un prezi para que sepas más sobre las fuerzas en física.

http://prezi.com/bvdokad77elb/?utm_campaign=share&utm_medium=copy&rc=ex0share

Fuerza: La fuerza es todo aquello capas de deformar un cuerpo o modificar su estado de reposo o de movimiento.

Para que exista una fuerza es necesaria la presencia de dos cuerpos que interaccionen.

La fuerza del palo modifica el estado de reposo de la bola.	La fuerza del guante modifica la dirección del movimiento de la pelota.	La fuerza del martillo deforma el cuerpo (hasta tal punto que lo rompe)

Las fuerzas se representan mediante flechas (Vectores). Los segmentos de recta indican la dirección y el extremo acabado en la punta de la flecha, el sentido,

Vector: Un vector es la interpretación de una magnitud que se compone de un modulo, una dirección, un sentido y un punto de aplicación.  

Sobre un cuerpo actúan dos tipos de fuerzas: De contacto y a distancia

Fuerza de contacto: Son las que se producen cuando los dos cuerpos están en contacto. Un ejemplo de ello seria al momento de mover una caja, como se muestra en la imagen.

Fuerza a distancia: Son aquellas que se producen cuando los cuerpos no están en contacto. Un ejemplo de ello son los imanes que con su fuerza magnética se atraen o se retraen.

Fuerza resultante: Si sobre un cuerpo actúan varias fuerzas se pueden sumar las mismas de forma vectorial (como suma de vectores) obteniendo una fuerza resultante, es decir equivalente a todas las demás. Si la resultante de fuerzas es igual a cero, el efecto es el mismo que si no hubiera fuerzas aplicadas: el cuerpo se mantiene en reposo o con movimiento rectilíneo uniforme, es decir que no modifica su velocidad.

En la mayoría de los casos no tenemos las coordenadas de los vectores sino que tenemos su módulo y el ángulo con el que la fuerza está aplicada. Para sumar las fuerzas en este caso es necesario des componerlas proyectándolas sobre los ejes y luego volver a componerlas en una resultante (composición y descomposición de fuerzas).

Fuerza equilibreante: Se llama fuerza equilibrante a una fuerza con mismo módulo y dirección que la resultante (en caso de que sea distinta de cero) pero de sentido contrario. Es la fuerza que equilibra el sistema. Sumando vectorialmente a todas las fuerzas (es decir a la resultante) con la equilibrante se obtiene cero, lo que significa que no hay fuerza neta aplicada.

Métodos gráficos de suman vectorial

Para utilizar métodos gráficos en la suma o resta de vectores, es necesario representar las cantidades en una escala de medición manipulable. Es decir, podemos representar un vector velocidad de 10 m/s hacia el norte con una flecha indicando hacia el eje y positivo que mida 10 cm, en la cual, cada cm representa una unidad de magnitud real para la cantidad (1 m/s).

El vector que resulta de operar dos o más vectores, es conocido como el vector resultante, o simplemente la resultante .

El método del paralelogramo permite sumar dos vectores de manera sencilla. Consiste en colocar los dos vectores, con su magnitud a escala, dirección y sentido originales, en el origen, de manera que los dos vectores inicien en el mismo punto. Los dos vectores forman dos lados adyacentes del paralelogramo. Los otros lados se construyen trazando lineas paralelas a los vectores opuestos de igual longitud. El vector suma resultante se representa a escala mediante un segmento de recta dado por la diagonal del paralelogramo, partiendo del origen en el que se unen los vectores hasta la intersección de las paralelas trazadas.

Ejemplo. Una bicicleta parte desde un taller de reparación y se desplaza (4 m, 30º) y luego (3 m, 0º). Encuentre el desplazamiento total de la bicicleta, indicando la dirección tomada desde el taller.

El desplazamiento total se da en dos tramos. Cada tramo desplazado se representa por los vectores d1 y d2. El desplazamiento total es D = d1 y d2.

Los dos vectores son dibujados a la misma escala, y se colocan en el mismo origen. Luego se trazan las lineas paralelas.

Si medimos con una regla, a la escala dada, el tamaño del vector resultante debe dar aproximadamente 6.75 unidades de la escala; es decir, la magnitud del vector desplazamiento total es de 6.75 m.

La medida de la dirección se toma con la ayuda de un transportador, y debe dar aproximadamente 17º desde el origen propuesto. El sentido del vector resultante es positivo, según el marco de referencia común (plano cartesiano, hacia x positivo y hacia y positivo). Entonces como resultado, la bicicleta se desplaza (6.75 m,17º).